Quadratures
Quadratures
Introduction
A quadrature is just a name we use to describe methods of numerical integration
In this chapter we will look at some simple methods such as the trapezium rule, which you will already be familiar with and then we will consider some more sophisticated developments, such as Simpson's and Boole's rule, which interpolate function points with polynomials of increasing degree
Finally we will look at Gaussian quadratures where the assumption of evenly spaced abscissa points is dropped and a more general form of quadrature is developed which can produce remarkably accurate results with relatively little calculation
Very basic quadrature methods
The most basic form of numerical integration is called the left point rule: In this case we simply divide the function into intervals of width $\Delta x$ and then add up the area of the rectangles width: $\Delta x$ and height: $f(x_i)$, where $x_i$ is the value of $x$ at the left of the interval
This gives: $\int_{a}^{b}f(x) dx \approx \Delta x \times \left(f(x_0)+f(x_1)+...+f(x_{n-1})\right)$
where $a=x_0$, $b=x_n$ and the $x_i$s are evenly spaced across the interval.
The right point rule and the mid-point rule follow by analogy
Clearly these methods are very primitive and it is easy to improve on them
The Trapezium Rule
The trapezium rule represents the first level of sophistication in the numerical calculation of integrals
consider the problem of how to calculate the area under the curve: $y=e^{-x} \times sin x$ between $0$ and $\pi$
The following graph shows how we could use a series of trapeziums to estimate this integral
We can easily see that the area under the trapeziums reduces to:
$A=\frac{\pi}{8} \times \left(f(0) + 2f(\frac{\pi}{4}) + 2f(\frac{\pi}{2}) + 2f(\frac{3\pi}{4}) + f(\pi) \right)$
So more generally the trapezium rule is given by:
$\int_{a}^{b} f(x) dx \approx \frac{\Delta x}{2} \times \left(f(x_0)+2f(x_1)+2f(x_2)+...+2f(x_{n-1})+f(x_{n})\right)$
Write a VBA routine to approximate the integral of a general function between abscissas $a$ and $b$ with any given number of intervals using the trapezium rule
Approximate the area under $y=e^{-x} \times sin x$ between $0$ and $\pi$ using 4, 12 and 120 intervals
Simpson's Rule
Suppose instead of fitting straight line segments to our function we attempt to find a better fit by fitting quadratic segments
Look at the same function below (grey) with two black quadratics fitted to the first three and last three calculated function points
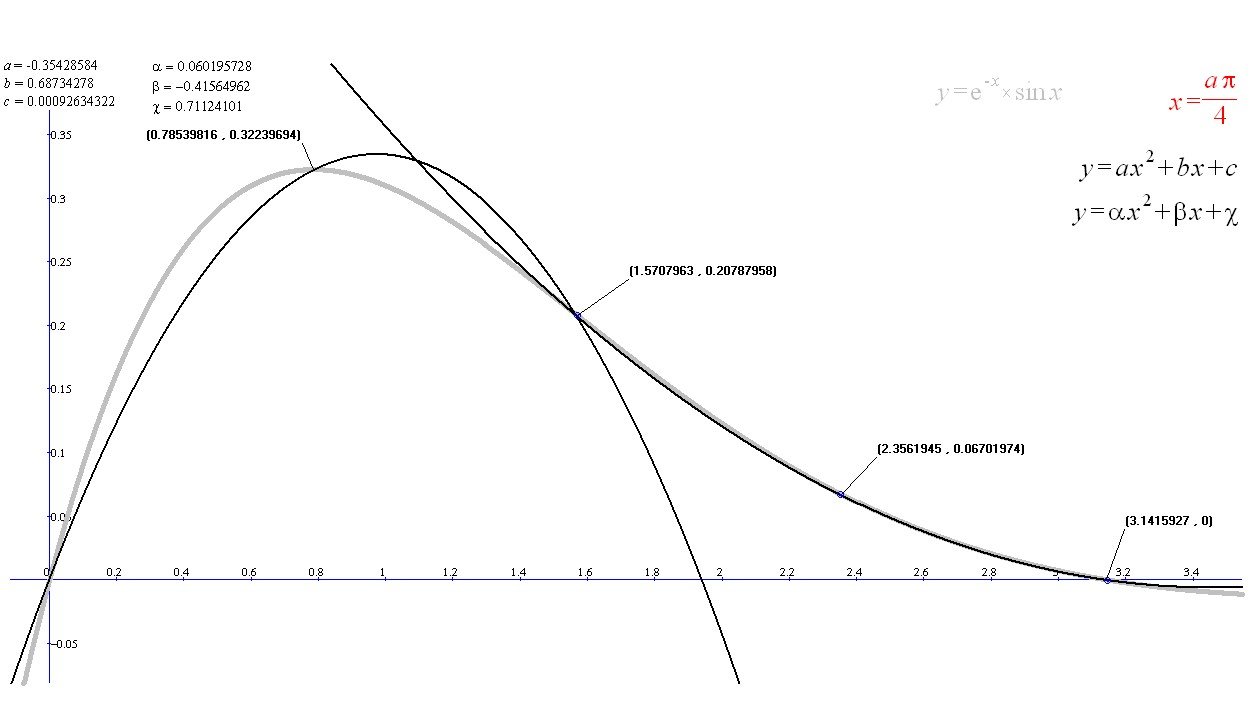
By considering a function $f$ on the interval $[-\theta, \theta ]$ and using abscissa points $-\theta$, $0$ and $\theta$, calculate the quadratic which will interpolate the three points
Using basic calculus, calculate the area under this quadratic on the interval $[-\theta, \theta ]$ as a function of $\theta$, $f(-\theta)$, $f(0)$ and $f(\theta)$
This leads us to Simpson's Rule which is stated generally as:
$\int_{a}^{b} f(x) dx \approx \frac{\Delta x}{3} \times \left(f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+...+2f(x_{n-2})+4f(x_{n-1})+f(x_{n})\right)$
Write a VBA routine to approximate the integral of a general function between abscissas $a$ and $b$ with any given number of intervals using Simpson's Rule
Approximate the area under $y=e^{-x} \times sin x$ between $0$ and $\pi$ using 4, 12 and 120 intervals using Simpson's Rule (2,6 and 60 quadratic segments)
Simpson's three eighths Rule
The next level is to fit cubic segments
Look at the same function again (grey) with the red cubic fitted to four calculated function points

The principles are exactly the same but the algebra is a bit more complicated, so Simpson's 3/8ths Rule over a $3\Delta x$ interval can be expressed as:
$\int_{a}^{b} f(x) dx \approx \frac{3\Delta x}{8} \times \left(f(x_0)+3f(x_1)+3f(x_2)+f(x_3)\right)$
Write a single VBA routine to approximate the integral of a general function between abscissas $a$ and $b$ with any given number of intervals and allowing the user to choose between the methods given so far
Approximate the area under $y=e^{-x} \times sin x$ between $0$ and $\pi$ using 3, 6, 12 and 120 intervals using Simpson's 3/8ths Rule
Boole's Rule
The next level is to fit quartic segments
This time the interpolating function is a quartic
The principles are again the same, so Boole's Rule over $4\Delta x$ interval can be expressed as:
$\int_{a}^{b} f(x) dx \approx \frac{\Delta x}{45} \times \left(14f(x_0)+64f(x_1)+24f(x_2)+64f(x_3)+14f(x_4)\right)$
Extend your VBA routine to include Boole's Rule
Approximate the area under $y=e^{-x} \times sin x$ between $0$ and $\pi$ using 4, 12 and 120 intervals using Boole's Rule
Programming Extensions
There are a number of things you should now do to tidy up your routine
- Ensure the routine checks for an appropriate number of intervals for each integration method
- You could splice different methods where $n$ does not fit
- You could include an option to leave out $n$ and let the routine try different values until some convergence criterion is reached